


Next: Future Work
Up: Reconfigurable Cryptography A Hardware
Previous: Results
The speed and density of the compiled algorithms compares well with
hand-written VHDL. The Synopsys tools are very sensitive to the
manner in which the hardware description is expressed [SWA95],
and we are confident that closer examination of the generated code
will disclose ways to make up the current 20% performance penalty of
the compiled code. The state-machine generation algorithm utilizing
the SSA form information appears to be robust and efficient.
The future of FPGAs in brute-force cracking machines does not appear
as rosy. Although the 514,000 key per second cracking rate of the
Tea2 design (and the presumably similar speed of
Tea1) compares favorably with the software speeds listed in
table 2, it is unimpressive compared to more
sophisticated implementations on faster processors or custom hardware.
Table 5 shows that the FPGA implementations discussed
here are a hundred times slower than a custom CMOS design. Wiener's
50 million key/s design was manufacturable for less than $11/chip; the
Xilinx XC4010 considered here costs about $100.![[*]](foot_motif.gif) The added algorithmic flexibility of the FPGA approach
does not seem to justify the three orders of magnitude speed-cost
ratio disadvantage. Wiener's $1 million brute-force cracking machine
would cost $1 billion if it were to use reconfigurable devices.
Wayner's content-addressable memory scheme [Way93] seems more
practical; however it is unclear whether it can handle addition-based
algorithms such as TEA and RC5.
The added algorithmic flexibility of the FPGA approach
does not seem to justify the three orders of magnitude speed-cost
ratio disadvantage. Wiener's $1 million brute-force cracking machine
would cost $1 billion if it were to use reconfigurable devices.
Wayner's content-addressable memory scheme [Way93] seems more
practical; however it is unclear whether it can handle addition-based
algorithms such as TEA and RC5.
Table 5:
Realistic speed comparison.
| Technology |
Speed (keys/s) |
Notes |
| FPGA |
514k |
Best TEA results |
Software |
1,660k |
175MHz MIPS R10000, bitsliced |
Custom hardware |
50,000k |
0.8 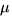 m standard-cell CMOS m standard-cell CMOS |
 From author's experiments with the DES Challenge
client from http://www.frii.com/rcv/deschall.htm.
From author's experiments with the DES Challenge
client from http://www.frii.com/rcv/deschall.htm.
 From [Wie94]
From [Wie94]



Next: Future Work
Up: Reconfigurable Cryptography A Hardware
Previous: Results
C. Scott Ananian
10/11/1997
![[*]](foot_motif.gif) The added algorithmic flexibility of the FPGA approach
does not seem to justify the three orders of magnitude speed-cost
ratio disadvantage. Wiener's $1 million brute-force cracking machine
would cost $1 billion if it were to use reconfigurable devices.
Wayner's content-addressable memory scheme [Way93] seems more
practical; however it is unclear whether it can handle addition-based
algorithms such as TEA and RC5.
The added algorithmic flexibility of the FPGA approach
does not seem to justify the three orders of magnitude speed-cost
ratio disadvantage. Wiener's $1 million brute-force cracking machine
would cost $1 billion if it were to use reconfigurable devices.
Wayner's content-addressable memory scheme [Way93] seems more
practical; however it is unclear whether it can handle addition-based
algorithms such as TEA and RC5.