



| C. Scott home | . | MAS863 projects |
"How a computer scientist makes stained glass."
We start with scanned photographs of the two Art Nouveau windows by Arnold Lyongrün: (as the images came from a compilation, it's not entirely clear that these particular windows didn't actually come from this book of "Bunte Verglasungen"-style works.)




We next manually extract a black-and-white outline. "Select by color" in the GIMP works fairly well, as does thresholding, but manual intervention is needed to select appropriate thresholds and ensure the resulting skeleton is properly connected.
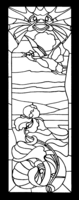



From this point on, the software performs all steps automatically. The detail above showed that the extracted outline is pixellated. We use the "polygon-tracer" potrace to convert the outline into a optimal collection of smooth curves which would, if rasterized, produce the bitmap. The algorithm is described in detail in this paper by Peter Selinger.
Stained glass is held together by H-shaped lead channels called came. The black strips in photographs of stained glass thus show the outline of the outside of the H; we actually want a much smaller (1/16" or 1/32", depending on assembly method) gap between our cut pieces. We address this discrepancy by extracting a "centerline" from our vectorized outline, and then offsetting from the centerline by the appropriate exact gap amount.
We will use the medial axis transform (MAT) to extract our centerline, a process called "skeletonization". The MAT can be approximated by portions of the Voronoi Diagram, if the boundary of the shape is approximately uniformly sampled. We form a similar approximation by tracing centers of the Delaunay triangulation of the boundary polygon; the Delaunay triangulation is dual to the Voronoi diagram.
Our first step is to uniformly sample the boundary.
We read in the SVG-format
boundary descriptions produced by potrace with the
Batik library. We then
finely subdivide the curves and generate boundary points and edges.
We then use the netlib Triangle program, written by Jonathan Richard Shewchuk, to compute the conforming Delaunay triangulation of the boundary points, subdividing edges as necessary to ensure that the boundary edges are also Delaunay edges.
Triangle isn't very smart about distinguishing between the inside
and outside of boundaries, so the first thing we do in our
Assemble class, after reading in its result files, is to
remove "interior" triangles from the result.
We trace the center of the Delaunay triangles to generate a (disconnected) centerline, represented as a graph between nodes.
We then use a path-searching algorithm to find the smallest cycles in the graph, which represent individual pieces of stained glass. I initially used a priority-first search through the graph using path-length as priority, but you can quickly convince yourself that the "innermost" boundary is not necessarily the shortest. Imagine, for instance, a figure-eight. You can replace the center bar of the figure eight with an arbitrarily squiggly line that will have an arbitrarily large path-length. But you still want the 'regions' found to be the bottom and top cut-outs: you don't want to find instead the outside boundary of the figure-eight just because it is 'shortest'.
Note also that the MAT transform typically results in "spurs" or "hairs" off the centerline, pointing at every convex vertex; we want our cycle-finding algorithm to identify and remove these as well. (These stubs are easy to see on the four outermost corners of the full-size output below. They are colored green, indicating that they are part of the MAT but not part of the cyclic regions, which are yellow-orange.)
Our improved (i.e. "correct"!) algorithm solves these problems with what is basically a "right-hand" maze search. We represent every undirected edge as a pair of directed edges in opposite directions. We then iteratively pick an unmarked edge and search forward, always picking the clockwise-most path when we come to a junction. When we find an edge we've already traversed, we've identified a cycle: record it mark all edges involved. If the edge found isn't the one we started with, there's an acyclic stub from our starting point to the edge we found; discard it and mark the edges. If we run out of path without finding a cycle, we've traced another stub; discard it and mark edges. When we run out of unmarked edges, we've found all cycles. (Thanks to Viktor Kuncak for pointing me in the right direction for this algorithm.)
We don't want to have to create plunge cuts through the glass for every individual piece, so we now connect adjacent regions with small pieces of sprue. We optimally place sprue on the longest edges connecting disconnected regions, on the theory that the sprue will be easier to cut apart and be less likely to obscure important geometry on long edges. The result is a single continuous toolpath which outlines all pieces.
We then offset our regions by 1/16" or 1/32" to leave the proper allowance for assembly.
We emit the final result as a DXF file. While I familiarize myself with stained glass technique, I'm only attempting to construct an 11x14 portion of the original window, so we also perform trimming (with boolean area operations) on the original file before emitting it. Unfortunately, this can cause some regions connected with sprue to become disconnected. The images below show some triangular pieces of sprue which were manually added to reconnect the cuts into a single toolpath.
Final path, postscript format: mallard1-4.ps, mallard2-4.ps.
Final path, DXF format: mallard1-4.dxf, mallard2-4.dxf.
We can also use the regions and the original color image to identify colors for each stained glass piece. We first use a 1-pixel-expanded version of the initially-extracted polygonal boundary to distinguish "lead" from "glass" areas of the color image, so that our colors are not polluted by the black "lead" pixels. We then compute a average color for all non-lead pixels in each region.
It turns out that some vendors
of stained glass have color images for each glass type available
on-line. For example,
Spectrum Glass uses a
numbering
system which would identify Medium
Green Cathedral Hammered Glass as 9971-123H.
An image of this glass can be fetched from
http://www.warner-criv.com/images/products/medium/9971-123H.jpg.
Alternatively, image files can be downloaded directly from
the manufacturer's FTP site.
We perform a similar color averaging on these stock glass images to arrive at an average color. We can then supply a list of glass types "on hand" to the program, which will fetch the appropriate images from the net, determine "average colors" from these images, and then select a glass type from each region which most closely matches its computed color. The results (for a rather poor selection of colors "on hand") are shown below. PDFs were generated using Paul Mutton's excellent EpsGraphics2D package.
All source code used is available for
download under the terms of
the GNU GPL. Potrace is
available from potrace.sourceforge.net; triangle is included in the
download, but is also available from netlib, in the
voronoi directory.
cscott cscott.net
Copyright © 2004 C. Scott Ananian. cscott.net
Copyright © 2004 C. Scott Ananian.Verbatim copying and distribution is permitted in any medium, provided this notice is preserved. |